Last updated on January 9th, 2024 , 02:03 pm
Jump To
Expected Move Definition: The “expected move” of a security represents the amount that a stock is expected to either rise or fall from its current market price based on its current level of implied volatility. This number is very helpful when trading options on both stocks and ETFs.
A stock’s “expected move” represents the one standard deviation expected range for a stock’s price in the future.
A one standard deviation range encompasses 68% of the expected outcomes, so a stock’s expected move is the magnitude of that stock’s future price movements with 68% certainty.
There are three variables that go into the expected move formula:
1) The current stock price
2) The stock’s implied volatility
3) The desired expected move period (expressed as the number of days)
Since a stock can have multiple implied volatilities depending on the expiration cycle, it’s important to use the implied volatility of the options in the expiration cycle closest to the desired time period. For example, when looking at the option chain on a stock, you might see something similar to the following:
If you wanted to calculate the expected move for this stock over the next 75 days, it wouldn’t make sense to use the 7-day implied volatility.
Instead, it would be better to use the implied volatility of the 70-day options. Why? Because the 7-day implied volatility is 27.50% while the 70-day implied volatility is 24.50%. If you used 27.50% for a 70-day expected move calculation, the result would be overstated.

New to options trading? Learn the essential concepts of options trading with our FREE 160+ page Options Trading for Beginners PDF.
Expected Move Formula
Now that you know some of the best practices, it’s time to perform some calculations. Here is the expected move formula:
If you wish to use trading days instead of calendar days, just change the denominator from 365 to 252, since there are 252 trading days in a year. Both calculations will result in virtually the same number.
Using the formula and table from above, let’s calculate the expected move for each time period. Let’s assume the current stock price is $200:
Expected Move Example (stock at $200)
The expected moves in this table suggest the following:
➜ The 7-day option prices are implying a 68% probability that the stock price is ±$7.62 from $200 in seven days (between $192.38 and $207.62).
➜ The 35-day option prices are implying a 68% probability that the stock price is ±$15.64 from $200 in 35 days (between $184.36 and $215.64).
➜ The 70-day option prices are implying a 68% probability that the stock price is ±$21.46 from $200 in 70 days (between $178.54 and $221.46).
➜ The 126-day option prices are implying a 68% probability the stock price is ±$30.55 from $200 in 126 days (between $169.45 and $230.55).
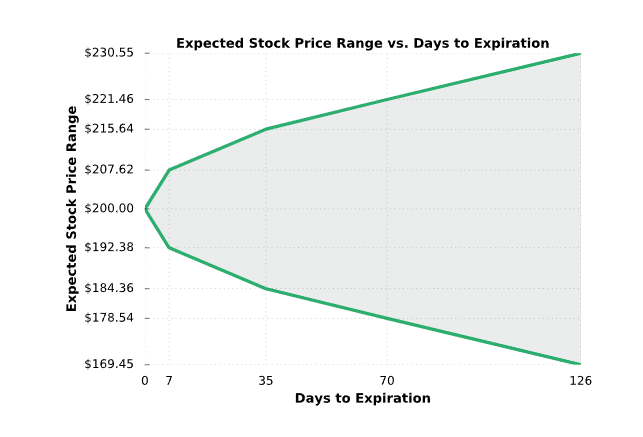
The following chart serves as a visualization for the table above:
Calculating the Expected Move With Straddles
This calculation involves taking 85% of the value of the front-month at-the-money (ATM) straddle. The resulting figure is a good ballpark number to determine a stocks expected move.
Why does this matter to you as an options trader? Knowing how much a stock’s price is expected to fluctuate over various time periods can give you a reasonable expectation for a stock’s future prices. Additionally, if you want to calculate a stock’s expected range over a specific period of time, you have the ability to do so.
Expected Move FAQs
The expected move tells us how much a stock, ETF or index is forecasted to either rise or fall from its current price. The expected move is derived from calculations involving implied volatility and front month option value.
The expected move can be calculated simply by multiplying the front month straddle by 85%. This straddle must be comprised of at-the-money options.
projectfinance Options Tutorials

About the Author
Chris Butler received his Bachelor’s degree in Finance from DePaul University and has nine years of experience in the financial markets.
Chris started the projectfinance YouTube channel in 2016, which has accumulated over 25 million views from investors globally.
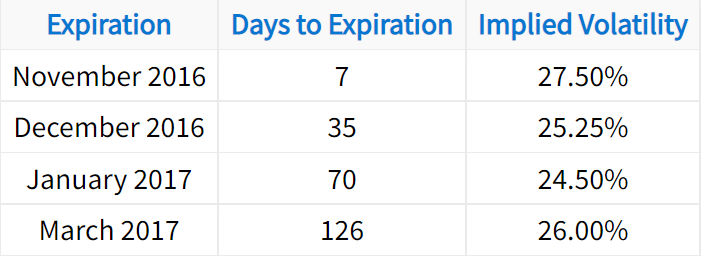
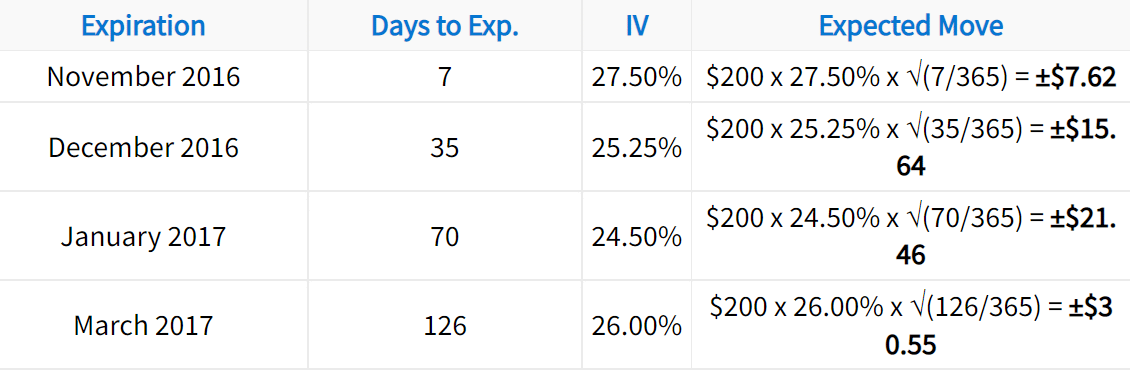




2 thoughts on “Expected Move Explained: Options Trading”
What if the stock price is not trading at the strike price when determining the “at-the-money” straddle? Like if the stock is at $132 and the only strike prices are $130 and $135? Which ones do you use?
Thanks for the question Hank. This can be tricky indeed. If the stock is trading in between the two strike prices, you can just use the average of the two straddles. Alternatively, you can use the equation in this article. Hope this helps!
Mike