Last updated on April 29th, 2022 , 06:02 am
The delta of an option expresses that option’s expected price change relative to movements in the stock price. For example, a +0.50 delta call option is expected to gain $0.50 in value when the stock price increases by $1. Conversely, that same option is expected to lose $0.50 when the stock price falls by $1.
However, it’s important to know how that option price change translates to profits and losses for your position, especially when trading complex positions with more than one option. Position delta takes things a step further and estimates the profits or losses on an entire option position relative to $1 changes in the stock price.
Care to watch the video instead? Check it out below!
Jump To
Option Delta Chain
In the above options chain, the call price should increase from $10 to $10.75 with a $1 increase in the underlying stock price, and decrease from $10 to $9.25 with a $1 decrease in the stock price.
But how does this translate to profits or losses for a trader with -2 contracts (short two contracts)?
Since this trader is short the call options, they profit from price decreases. More specifically, a decrease from $10 to $9.25 represents a $0.75 profit per option contract.
Recall that an option represents 100 shares of stock, so we need to multiply the change in the option price by 100 to solve for the actual return in dollars:
($10 sale price – $9.25 current price) x 100 = +$75
Lastly, the trader in this example is short two contracts, so the $75 profit becomes a $150 profit when multiplying by two contracts.
Working through this example, we learn that the trader is expected to profit by $150 when the stock price decreases by $1. Therefore, the trader’s position delta in this example is -150, as a $1 increase in the stock price should lead to $150 in losses, and a $1 decrease in the stock price should result in a profit of $150.
So, while the option’s delta is +0.75, it doesn’t indicate the expected profits or losses for a trader who is short two contracts. Analyzing the overall delta of the position solves this problem by converting an option’s delta into the expected profits or losses for a specific position when the stock price changes.
Alright, so you know the basic idea behind position delta. Next, we’ll discuss the formula you can use to calculate the delta for any option position.
Need a brokerage account?
We trade with tastyworks because of their trader-friendly commissions ($10 options commission cap and close trades for free) and easy-to-use platform.
Sign up with tastyworks and earn up to $500 for funding your first account ($200 for funding $2,000 -OR- $500 for funding $10,000).
Offer valid through 2/28/2022
Calculating Position Delta
To calculate the position delta for a standard equity option position, the following formula can be used:
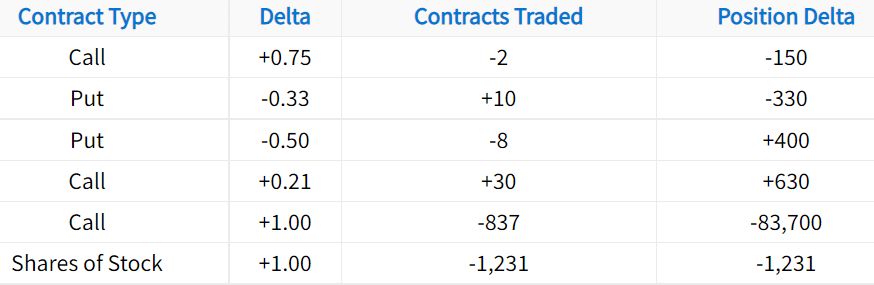
The following table demonstrates this formula applied to various simple option positions:
It’s important to note that when selling options or shares of stock short, the number of contracts traded is a negative number. Using negative numbers to indicate short positions is conventional in the trading industry.
Here are the main points to take away from this table:
➜ When short contracts (negative number of contracts), the position delta will have the opposite sign of the option’s delta.
➜ A share of stock has a delta of +1.00, which results in positive position delta when buying shares and negative delta when shorting shares.
➜ A positive position delta represents a position that profits from stock price increases and loses money from stock price decreases. For example, the +630 delta position is expected to profit by $630 with a $1 increase in the share price and lose $630 after a $1 decrease in the share price.
➜ A negative position delta represents a position that profits from stock price decreases and loses money from stock price increases. For example, the -83,700 delta position is expected to lose $83,700 with a $1 increase in the share price and profit by $83,700 with a $1 drop in the share price.
At this point, we’ve discussed position delta and how to calculate it for simple positions. In the next section, we’ll calculate the delta of more complex positions.
Position Delta of Complex Positions
Calculating the delta of a more complex option position is simple. All you have to do is sum up the position delta for each option in the strategy. As an example, let’s calculate the overall delta for a hypothetical long call spread:
In this example, the five long calls generate a delta of +375 while the five short calls generate a delta of -125. Adding these two deltas together leaves us with a net position delta of +250.
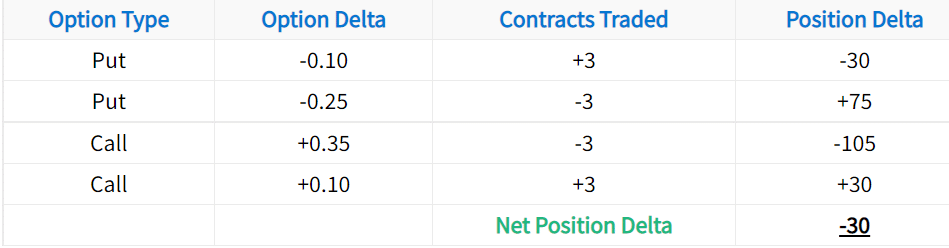
Next, we’ll calculate the overall delta for a hypothetical short iron condor option strategy, which is a strategy that includes four different options:
In this example, the long puts and calls generate -30 and +30 deltas respectively, resulting in zero delta exposure. However, a 0.35 call and a -0.25 put are sold, resulting in a slightly bearish bias. The net position delta of this iron condor is -30, which indicates an expected $30 profit when the stock price falls by $1 and a $30 loss when the stock rises by $1.
Real Trade Examples
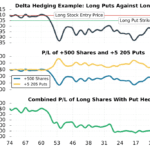
In the following example, we’ll take a look at the delta and profit/loss of an option position that recently traded in the market. We’ll visualize the performance of the position and examine the accuracy of position delta.
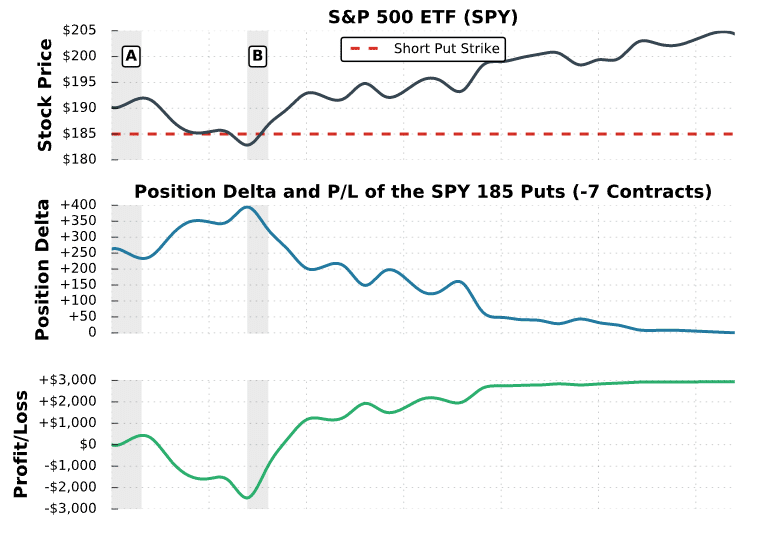
SPY Short Puts
In this example, we’ll examine the position delta and P/L of a short put option position in SPY. The position was initiated in February of 2016 and the options expired in March of 2016.
To make things easier for you, we’ve shaded two regions that demonstrate the accuracy of position delta. The following table compares the expected vs. actual P/L based on the position delta in each region.
As we can see here, the actual P/L was fairly close to the expected P/L that was projected by the position delta. The differences in each case can be attributed to the fact that position delta changes when the stock price changes. Additionally, other factors like theta decay and changes in implied volatility also contribute to P/L.
What is Delta Neutral?
In options trading, delta neutral is a strategy used to balance out both positive and negative delta. This is accomplished through both buying and selling shares of the underlying stock.
The goal of this strategy (used by both market makers and professional option traders) is to offset the risk that comes with holding an inventory of call options and put options.
In a true delta neutral portfolio, the net delta of an entire position will be zero.
Position Delta FAQs
In options trading, the delta of a portfolio tells us how sensitive a security is to changes in the underlying price. Assuming all other variables are constant, delta tells us the amount an option price is expected to move based on a $1 future change in the underlying stock price.
There is no such things as a “good” delta in options. Traders who want to take on high risk generally have larger net deltas while traders wanting low risk, or a reduction in risk, have deltas approaching zero.
Next Lesson
Additional Resources
projectfinance Options Tutorials
About the Author
Chris Butler received his Bachelor’s degree in Finance from DePaul University and has nine years of experience in the financial markets.
Chris started the projectfinance YouTube channel in 2016, which has accumulated over 25 million views from investors globally.
2 thoughts on “What is Position Delta? | Options Trading Concept Guide”
Thanks for the read!
Quick question – do high deltas mean that a trade has a higher probability of success?
Thanks!
Thanks for the question Pauline!
In-the-money options have a greater probability of success than out-of-the-money options. As we learned, in-the-money options have higher deltas than out-of-the-money options. Therefore, higher deltas do indeed mean a higher probability of success. However, higher delta options also cost more money to purchase, and therefore have greater risk!
Mike